Математика микширования

  Александр ФЕДОРОВ
Музыкальное Оборудование
ноябрь 2000

В спецификациях современных DSP все чаще встречается фраза “внутренняя обработка 32-разрядная с плавающей запятой”. Микшеры таких программ, как Cubase VST, Cakewalk, WaveLab, CoolEdit также работают в этом формате. Напрашивается вопрос: а почему, собственно, 32 бита, да еще с плавающей запятой?

Разобраться в вопросе меня побудили и вовсе обвинительные заключения некоторых пользователей, проводивших тестирование алгоритмов микширования указанных программ, в частности, Cubase VST. Результаты тестов говорили о том, что при микшировании происходит внутренняя перегрузка.

Для примера: в одном из тестов были взяты три программно сгенерированные синусоиды с частотами 400, 1000 и 6500 Гц соответственно и уровнем -6 дБ. В Cubase 3.7 импортировались три аудио файла с этими тестовыми сигналами разрешением 24 бита и частотой дискретизации 48 кГц. Затем все это микшировалось (при нулевых положениях фейдеров линеек и мастер-фейдеров) на одну дорожку с помощью команды Create File мастер-секции. Миксдаун (также с разрешением 24 бита и частотой дискретизации 48 кГц) звучал отвратительно, так, как будто сигнал был обработан эффектом Fuzz. В его спектре появлялось множество посторонних гармоник (рис. 21), расположение которых очень схоже с тем, какое наблюдается при превышении цифровым сигналом уровня 0 дБ.

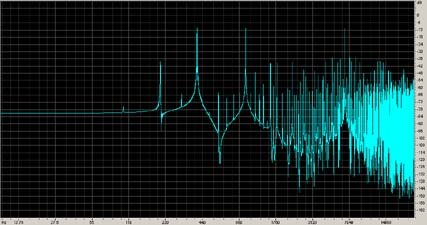
Я проделал подобный тест и в Cubase VST 32 5.0. При нулевых положениях фейдеров наблюдался тот же перегруз и та же невеселая спектральная картина. Затем я смикшировал эти синусоиды в CoolEdit 2000. Результат тот же. В WaveLab 3.0 (последовательной вставкой в начало файла в режиме Mix) — один в один. Все это навело меня на мысль: а, может, уровень микса данных сигналов действительно превышает 0 дБ? Для цифрового звука это превышение моментально приводит к многочисленным “клипам”, которые все и портят.

Из школьного курса физики известно, что мгновенная амплитуда гармонического колебания:

Алгоритм микширования заключается в простом сложении мгновенных отсчетов сигнала, поэтому суммарная мгновенная амплитуда в нашем случае будет равна: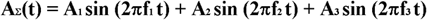

Чтобы не возиться с громоздкими числами, отражающими реальное значение семплов, примем максимально возможную амплитуду (соответствующую уровню 0 дБ) за единицу. Тогда амплитуда синусоиды с уровнем -6 дБ (как в нашем случае) будет равна 0,5: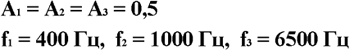

а полная формула микса станет такой:

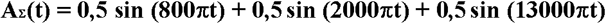
С помощью простой подстановки выясняется, что при некоторых значениях времени мгновенная амплитуда превышает единицу и происходит перегрузка. Например: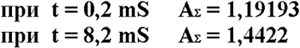

При большом увеличении волновой формы миксдауна в WaveLab эти цифры полностью подтверждаются. А посему вывод: для тестов алгоритма микширования указанные сигналы брать нельзя, так как без принудительного уменьшения их уровня перегрузка неизбежна. Это самое уменьшение уровня (в данном случае — на 4 дБ в мастер-секции либо на 2 дБ в каждом канале) позволяет получить замечательный миксдаун с посторонними гармониками на уровне порядка -150 дБ, возникающими вследствие дизеринга с 32 до 24 бит.

Противоречие налицо. С одной стороны, для избавления от цифровой перемодуляции нужно поддерживать низкий уровень дорожек, с другой — иметь максимально возможный уровень в файле для полного использования всех разрядов семпла.

Вот тут-то и проявляются преимущества 32-разрядной обработки сигнала с плавающей запятой.

Для начала давайте разберемся, как представить отсчет сигнала (семпл) числом с плавающей запятой. С целым числом все понятно: при разрешении 24 бита максимально возможная положительная амплитуда равна: 2^24-1 = +8.388.608, а отрицательная, соответственно, -8.388.608. Преобразование в формат с плавающей запятой происходит по формуле:

В случае максимальной амплитуды отсчета (+/-8.388.608 при разрядности 24 бита) амплитуда в формате плавающей запятой будет равна +/-1,0. Из этого вытекают два важных следствия.

1. Числа с плавающей запятой могут представлять гораздо более мелкие изменения уровня, чем младший бит (LSB) 24-разрядного числа. Например, семпл со значением +4.000.000 преобразуется в “плавающий” формат со значением 0,47683716. А семпл +4.000.001 — в 0,47683728. Если при обработке сигнала получается число, скажем, 0,47683723, то для преобразования его в целое приходится производить округление и выбирать: +4.000.000 или +4.000.001. Хотя ясно, что реальное значение находится где-то между ними.

2. Числа с плавающей запятой могут представлять уровни, большие 0 дБ. Действительно, раз уровню 0 дБ соответствует значение +/- 1,0, то вполне допустимы (и реально получаются при вычислениях) значения больше этого, — например, +/-1,5 или +/-2,0. В последнем случае уровень поднимается до +6 дБ. Соответственно увеличивается и динамический диапазон.

Конечно, уровень больше 0 дБ допустим только на внутренних стадиях работы алгоритмов (или при передаче данных между программными модулями, соединенными в цепь). На выходе (при выводе 24-разрядных целых чисел) мы не можем получить уровни, большие 0 dBFS. Кстати, в программе WaveLab можно указать каталог для временных файлов, куда будут сбрасываться результаты внутренней работы алгоритмов мастер-секции в формате 32 бита с плавающей запятой, с уровнем, превышающим 0 дБ.

При использовании чисел с плавающей запятой можно не беспокоиться о перегрузках при увеличении уровня, применении эквалайзеров, суммировании каналов и т. д. благодаря большому динамическому запасу (headroom). А вот когда дело доходит до обратного преобразования в целочисленный 24-разрядный формат (максимальное разрешение протоколов передачи данных между цифровыми устройствами), могут возникнуть проблемы. Если не выполнить это преобразование корректно (что недешево), с соответствующим масштабированием и дизерингом, то качество звукового тракта всей системы остается под вопросом.

Напоследок хочется привести мнение, которое высказал авторитетный специалист в области цифровых технологий и мастеринга Bob Katz.

“Многие специалисты считают, что применение чисел с плавающей запятой позволяет увеличить внутренний динамический диапазон во время вычислений. Измерения искажений, проведенные мной при сравнении “целочисленных” устройств и устройств, работающих в формате с плавающей запятой, показали, что на некоторых алгоритмах фильтрации последний тип устройств выдает меньшие искажения. На самом деле все зависит от подхода разработчиков к внутренней реализации DSP.

В наиболее дорогих и мощных процессорах производители дошли до использования во внутренних вычислениях “двойного разрешения” (48 бит в большинстве случаев), которое удваивает внутренний динамический диапазон. Некоторые специалисты считают, что при этом качество обработки выше, чем в случае 32-разрядного формата с плавающей запятой. Стоимость таких процессоров все еще очень высока, но прогресс не стоит на месте, и цены на них неизбежно будут падать.

Положение может измениться, как только производители начнут использовать 40-разрядные вычисления с плавающей запятой. Хотя, в целом, при использовании одинаковых алгоритмов эти два формата позволят получить примерно схожие результаты.

При работе с удвоенным внутренним разрешением в целочисленном формате разработчики запросто могут установить 24 дБ (или больше) внутреннего динамического запаса без потери исходного динамического диапазона. Операции над целыми числами можно упрекнуть только в накоплении ошибок округления от вычисления к вычислению.

В любом случае, достаточно парочки упрощений в алгоритме, здорово снижающих стоимость системы, как оба вида вычислений могут сойти “на нет”. В особенности это касается наиболее критичного этапа, когда окончательные цифры конвертируются в формат 24-разрядного целого числа. Здесь нужно целиком полагаться на честность производителя. Измерения искажений, проводимые в данных случаях, не могут дать полной картины происходящих в устройстве процессов, а также продемонстрировать те ухищрения, на которые пошел производитель для снижения цены”.